The Essential Guide to Explicit Instruction in Mathematics
A PRACTICAL EVIDENCE-INFORMED PAPER FOR TEACHERS AND SCHOOL LEADERS
There is plenty of debate about how mathematics should be taught and much of it is driven by anecdotes and ideology, rather than evidence. I was the textbook example of it. I thought the fix was engagement. More rich tasks. More hands-on investigations. Make maths enjoyable and the persistence will follow. Instead, I found myself frustrated when students drifted off or gave up quickly. Looking back, it was never a behaviour problem. It was an instruction problem. I’d given them tasks they didn’t have the skills or knowledge to complete, then blamed their focus instead of my design. I was asking them to solve problems with knowledge they didn’t yet have.
I believed the core problem in education was a lack of so-called “21st Century Skills” and that strengthening those skills would automatically lift learning. As Emeritus Professor, John Sweller has pointed out, “Did I not need critical and creative thinking until the 21st century?” What I quickly discovered was that students did not need broader skills first. They needed secure foundational knowledge and clear, explicit teaching because you cannot solve problems with knowledge you do not yet have.
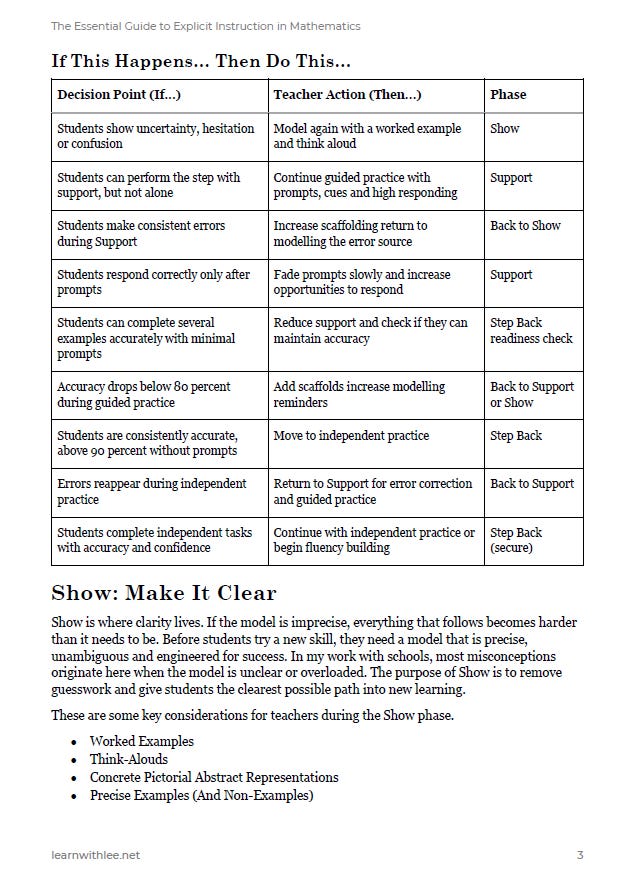
Explicit instruction is essential when students are first learning a new mathematical skill. In the acquisition stage, learners are unsure, inconsistent and easily overloaded. So, they need clear modelling, strong support and timely feedback. The Show, Support, Step Back framework provides a simple and practical structure for this phase. Show delivers precise modelling through strategies like worked examples and think-alouds. Support provides students prompts, opportunities to respond and immediate correction. Step Back removes the scaffolds once accuracy is secure so students can practise independently.
This guide demonstrates exactly how to do that in practice using Show, Support, Step Back as a reliable structure for teaching new content well. By the end, teachers will know how to model with precision, support students through guided practice and confidently decide when to step back.




My question is how does this framework allow students to understand the need for the mathematics? I would argue for the framework to be explore, discuss, show, support, step back. This would give students an opportunity to engage in a small exploration of the mathematics before being ultimately given the clear modeling. This, of course, would happen cyclically so that students are gaining mastery with one concept before exploring the next. The short explore activity allows students to engage with problem-solving and see how and why a new concept connects to what they have learned before. They still receive the clarity in the “show” that comes after.