When Explicit Instruction Turns Robotic

What happens when fidelity replaces decision making

Most teachers I work with understand the broad structure of explicit instruction.

Model clearly.
Guide practice.
Release students when they are ready.

The problem is not knowing what explicit instruction is supposed to look like. The problem is knowing what to do when it doesn’t go to plan. Because it rarely does.

Where explicit instruction breaks down

In theory, explicit instruction is often presented as a clean sequence.

1. I do

2. We do

3. You do

In practice, lessons are messier.

• Students hesitate.

• Errors appear.

• Accuracy fluctuates.

• Confidence comes and goes.

And in those moments, teachers are forced to make decisions in real time.

• Do I keep going?

• Do I go back?

• Do I add support?

• Do I remove it?

This is where explicit instruction either becomes powerful or mechanical.

Explicit instruction should power up teachers, not turn them into robots

Why resources are not the problem

Many schools respond to this complexity by providing teachers with detailed resources.

• Slide decks.

• Lesson sequences.

• Fully scripted programs.

• Textbooks with every step laid out.

This is often a sensible move.

It reduces teacher workload. It recognises that curriculum design requires a different level of expertise. It supports consistency across classrooms.

The problem is not the presence of resources. The problem is what happens when teachers are not clear on the key mechanisms of the program they are using.

Fidelity without understanding leads to rigidity

Schools want teachers to deliver programs with fidelity. Teachers want to do the right thing. So when uncertainty creeps in, a very predictable pattern emerges.

• Teachers click through every slide.

• They follow every page of the textbook.

• They hesitate to skip, adapt or return to earlier content.

Not because they are unwilling to think, but because they are unsure what is essential and what is flexible.

Without a clear mental model of how learning progresses, fidelity becomes compliance.

Explicit instruction turns into a procedure.

The missing link is decision making

This is the part of explicit instruction that is most often left implicit.

Explicit instruction is not a set of steps.
It is a decision making framework.

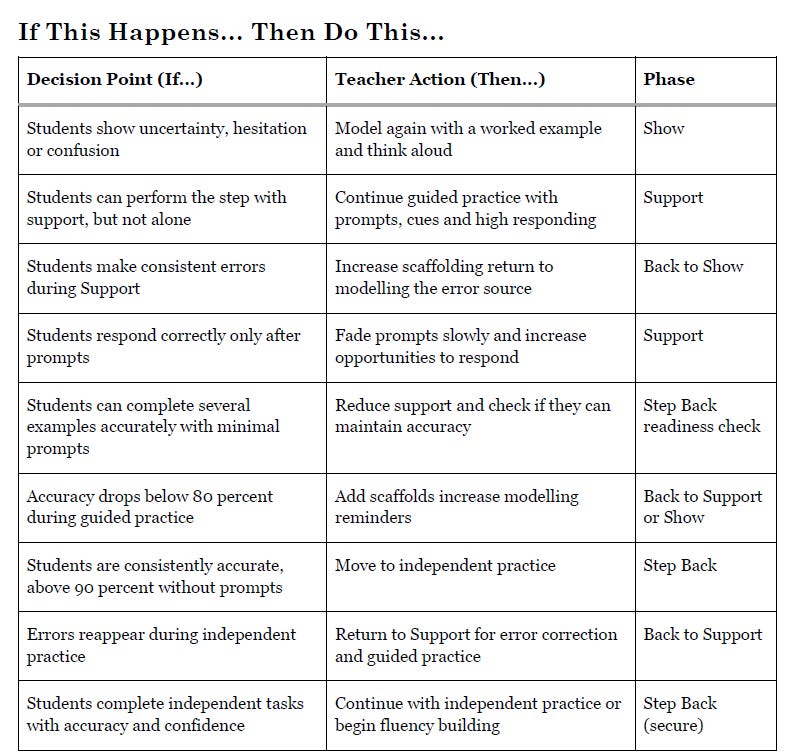
The phases matter, but the real work sits between them. If this happens, then do this.

Without that understanding, teachers cannot make principled decisions about what to keep, what to change and what to skip. They either over adapt and break the design, or under adapt and move on when students are not ready. In The Essential Guide to Explicit Instruction in Mathematics I describe the three key phases of explicit instruction as:

1. Show

2. Support

3. Step Back

This is the language that I use in this post. To learn more about it, make sure that you check out the full guide.

From The Essential Guide to Explicit Instruction in Mathematics

When students hesitate

If students show uncertainty, hesitation, or confusion, the issue is rarely motivation.

It is clarity.

At that point, moving on is not productive struggle. It is abandonment.

The correct response is to model again with a worked example and a clear think-aloud. This is not ignoring the resource. It is using it intelligently.

When students can only perform with support

If students can complete steps only with prompts, the message is clear.

They are still in the Support Phase.

No amount of clicking forward will fix that. Guided practice needs to continue, prompts need to be adjusted and opportunities to respond need to increase.

The resource does not decide when to move on. The evidence does.

When errors become consistent

Consistent errors point to a flaw in understanding, not effort.

At this point, adding more practice only entrenches the error. The correct move is to return to modelling and address the source directly.

Again, this may mean revisiting earlier slides or skipping ahead less quickly than planned. That is not a lack of fidelity. It is fidelity to learning.

When accuracy improves but relies on prompts

This is progress, but not readiness.

Here, prompts should fade deliberately. Support changes shape rather than disappearing altogether. This is a judgement call that no resource can make on its own. I wrote more about this here.

When students are ready

When students are consistently accurate, confident, and no longer reliant on prompts, independent practice becomes productive.

If errors reappear, the response is not frustration. It is information.

Return to Support. Correct. Adjust. Try again.

What this means for schools

Resources are necessary. Understanding is essential.

Schools that want both consistency and responsiveness need to make the decision rules explicit. Teachers need clarity about the mechanisms that matter, not just the materials to use.

Without that clarity, even the best designed resources can lead to rigid teaching.

With it, teachers can adapt with confidence and purpose.

Responsiveness requires content knowledge

What we are really talking about here is responsive teaching. However, having the ability to be responsive is not just a teaching skill. It also relies on content knowledge.

To respond well in the moment, teachers need to recognise what an error signals, which example to show next and how to adjust instruction without introducing confusion. That requires secure understanding of the content being taught.

This is particularly important in primary classrooms, where many teachers are non-specialists in mathematics. Asking teachers to be more responsive without supporting their subject knowledge places them in an impossible position. They are expected to make precise instructional decisions without the tools to do so.

Resources can help, but they cannot replace understanding. Slides and textbooks model one pathway, but they cannot anticipate every student response. When learning deviates from the expected route, teachers need to understand the content well enough to diagnose the issue and adjust.

If we want instruction to be responsive rather than robotic, we must also support teachers to enact responsiveness within specific curriculum areas, not just tell them to be more flexible.

A final thought

If explicit instruction ever feels robotic, it is usually because decision making has been replaced with compliance.

The real work of explicit instruction lives in the moments where teachers interpret evidence and choose what happens next.

That is what turns resources into instruction.

---

More info

If you would like to explore this thinking further, you can download the full guide that unpacks explicit instruction in mathematics, including modelling, practice, and decision making here.

And if you are looking for more structured support in understanding how these ideas connect at the lesson, curriculum, and school wide level, you can learn more about the Primary Maths Instruction Framework course here.

The focus is not on adding more resources, but on helping teachers and leaders understand what to keep, what to change, and why.